Ученически помощник

Видове операции с числа

Събиране:
- Събирането на обикновени числа става като съберете две или повече числа.
- Пример: 3 + 5 = 8
Изваждане:
- Изваждането на обикновени числа става като извадите едно цяло число от друго.
- Пример: 10 - 4 = 6
Умножение:
- Когато умножаваме две числа, ние ги събираме многократно.
- Пример: 3 . 5 = 15 3 х 5 = 15
Деление:
- Делението е като разделяме нещо на групи.
- Пример: 10:5 = 2 10/5 = 2 10÷5 = 2

Проценти

Видео урок на тема "Проценти" от МОН (с БНТ на училище, линк към YouTube)

Процентите са начин за изразяване на част от цялото, представен като стотинки. Те измерват отношението между една стойност и цялото количество, като се изразяват във форма на процент от 100. Процентите се използват широко за описание на увеличения, намаления, съотношения и други аспекти от числовата информация в по-лесен и удобен за разбиране начин.

Формиране на проценти:
- Пример: ако имаме 20 ябълки и искаме да изразим колко процента от тях са червени, ако 5 от тях са червени, тогава
- Формула: Процент червени ябълки = Брой червени ябълки ÷ Общ брой ябълки . 100 ==> Процент червени ябълки = ⁵/₂₀.100 = 25%
Процентно нарастване/намаляване:
- Когато число нараства спрямо друго, увеличението се изразява така: Нарастване = ново число - старо число Обаче, когато число намалява спрямо друго, намаление се изразява така: Намаление = старо число - ново число Процентът на нарастване или намаляване на число винаги се изразява спрямо основата на старото число. Или: %Нарастване = 100 ⋅ (ново число - старо число) ÷ старо число %Намаляване = 100 ⋅ (старо число - ново число) ÷ старо число
- Пример 1: Имали сте 80 пощенски марки и сте продължили да събирате докато общия брой на пощенските марки е достигнал 120. С колко процента са се увеличили марките ви?
  ^{120 - 80} / ₈₀ . 100 = 50%
- Пример 2: Имате 120 пощенски марки, с ваш приятел се съгласявате да размените неговата Лего игра за част от вашите марки. Той взема някои от марките, които му харесват. Вие преброявате, че са ви останали 100. С колко са намамели?
  ^{120 - 100} / ₁₂₀ . 100 = 16.67%

Декартова координатна система

Видео урок на тема "Правоъгълна координатна система" от МОН (с БНТ на училище, линк към YouTube)

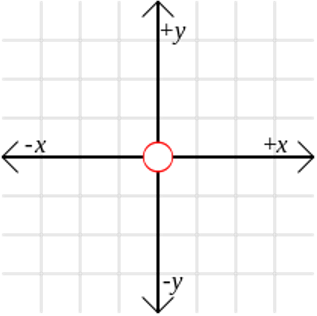
Декартовата координатна система е математически модел, предложен от френския математик Рене Декарт през 17-ти век. Тя предоставя графичен начин за описване на точки в равнината чрез две перпендикулярни координатни оси – X и Y. Ето някои от важните характеристики и концепции свързани с Декартовата координатна система:

Координатни оси:
- X-ос: Хоризонталната ос, представляваща абсцисата или хоризонталната координата (наляво или надясно).
- Y-ос: Вертикалната ос, представляваща ординатата или вертикалната координата (нагоре или надолу).
Нулева точка (начало на координатната система):
- Точката (0,0) е началото на координатната система и се нарича нулева точка.
Координати на точка:
- Точките в равнината се описват с двойка числа (x, y), където x е абсцисата, а y е ординатата.
Квадранти:
- Равнината е разделена на четири квадранта от координатните оси.
- Точките в квадрант I (горен десен) имат положителни x и y координати.
Графики на функции:
- Математични функции се представят чрез графици в Декартовата координатна система. Всяка функция има уникален график.

Видове дроби

Обикновени дроби

Те биват правилни и неправилни. Правилна е една дроб, когато числителят е по-малък от знаменателя, а неправилна - когато числителят е по-голям от знаменателя.

Дефиниция:
- Пример: a/b
- Обикновените дроби са числител и знаменател, разделени с черта, където a е числител, а b е знаменател.
Числител (a):
- Числото, което е горната част на дробта.
Знаменател (b):
- Числото, което е долната част на дробта и не може да бъде равно на нула.
Съкращаване:
- Дробите могат да се съкращават, като се раздели числителят и знаменателят на дробта с общ делител.
Операции с Дроби:
- Дробите могат да бъдат събирани, изваждани, умножавани и делени.

Смесени дроби

Дефиниция:
- Пример: 3¹/₂
- Смесена дроб се състои от цяло число, числител и знаменател. Например, 3¹/₂, където 3 е цялата част, 1 е числителят, а 2 е знаменателят.
Числител и Знаменател:
- Смесената дроба включва числител и знаменател, които се намират в обикновената дроб, част от израза
Цялостна Част
- Цялата част на смесената дроба е цялото число пред дробната част. Например, 4²/₃, 4 е цялата част.
Операции:
- Смесените дроби могат да бъдат събирани, изваждани, умножавани и делени. За удобство, те могат да бъдат преобразувани в обикновени дроби преди извършването на операциите.
Преобразуване в Обикновена Дроб:
- Смесената дроба може да бъде преобразувана в обикновена дроб, като се умножи цялата част по знаменателя и се добави числителят.
- Пример: 3¹/₄==> 3х4=12 (знаменател), 12+1=13 (числител) ===> получава се 3¹³/₄
- Знаменателят не се променя!

Десетични дроби

Дефиниция:
- Пример: 1.22 122,2245 0.2 a.bcd a,bcd
- Десетичните дроби са числа, които се представят чрез десетична дроб, т.е., дроб, където знаменателят е степен на 10. Формално, те се записват като a.bcd, където a е цялата част, а bcd е десетичната част.
Преобразуване в обикновена дроб:
- Десетичната дроб a.bcd може да се преобразува в обикновена дроб чрез следната формула: a.bcd = a + bcd/100
Събиране и изваждане:
- Десетичните дроби се събират и изваждат като съответно се слагат или изваждат десетичните части.
Умножение и деление:
- При умножение и деление, десетичните дроби се третират като обикновени дроби. При умножение, се умножават цялите части и десетичните части отделно. При деление, се умножава числителят на първата дроб по знаменателят на втората и обратно.
Приложение:
- Те се използват широко във всекидневни изчисления, финанси, инженерия, наука и други области, предоставяйки точно представяне на части от единица и позволявайки точни изчисления и мерки.

Видове уравнения

Линейни уравнения:
- Пример: ax+b=0
- Линейните уравнения представляват прави линии и имат степен на уравнението 1.
Квадратни уравнения:
- Пример: a²+ bx + c = 0
- Квадратните уравнения имат степен на уравнението 2 и могат да бъдат решени с формула на квадратните корени.
Системи от уравнения:
- Пример: ax + by = c dx + ey = f
- Системите от уравнения включват няколко уравнения и се решават обикновено за повече от една променлива.
Рационални уравнения:
- Пример: a/x + b/y = c
- Рационалните уравнения включват дроби и се решават чрез умножение и опростяване.
Експоненциални уравнения:
- Пример: log_b(x)=c
- Експоненциалните уравнения включват променливи в експоненциален вид.
Логаритмични уравнения:
- Пример: ax³ + bx² + cx + d = 0
- Логаритмичните уравнения включват логаритми на променливи.
Кубични уравнения:
- Пример: ∣ax+b∣=c
- Кубичните уравнения имат степен на уравнението 3.

Числото π (Пи)

В геометрията числото π (Пи) е приблизително равно на 3,14 или 22/7 (22 върху 7).
То се използва в различни формули и изрази, като например за изчисляване на обиколка и площ на кръг. Също така, то е важно в тригонометрията и анализа. Числото π е безкрайно число и има много интересни свойства, които го правят полезно и уникално в математиката.

Формули за съкратено умножение

Видео урок на тема "Формули за съкратено умножение" от МОН (с БНТ на училище, линк към YouTube)

(1): (a + b)² = a² + 2ab + b²

(2): (a - b)² = a² - 2ab + b²

(3): (a + b)³ = a³ + 3a²b + 3ab² + b³

(4): (a - b)³ = a³ - 3a²b + 3ab² - b³

(5): (a + b)(a - b) = a² - b²

(6): (a + b)(a² – ab + b²) = a³ + b³

(7): (a – b)(a² + ab + b²) = a³ – b³

Геометрични фигури

Кръг

Неща, които трябва да знаем за кръга:

Окръжността се определя от центъра и радиуса или диаметъра.
Окръжността е равна на 360°.
В окръжността има различни видове ъгли.

r	d	O
радиус	диаметър	център

Формула за лице:

S = π.r²

Формули за диаметър и радиус:

d = 2r
r = d/2

Формула за обиколка:

P = 2.π.r = π.d

Числото π

π = 3.14

Триъгълник

Неща, които трябва да знаем за триъгълника:

Сборът от ъглите в триъгълник е 180°.
Височината е перпендикулярът, спуснат от всеки връх към срещуположната страна на триъгълника.
Центърът на описаната окръжност се намира в пресечната точка на симетралите на страните.
Симетралата е перпендикулярна на страната и минава през нейната среда.
Центърът на вътрешно вписаната окръжност се намира в пресечната точка на ъглополовящите на ъглите.
Ъглополовящата дели ъгъла на две еднакви половини.
Медианата е отсечка, която свързва върха със средата на срещуположната му страна.

a,b,c	h_a	h_в	h_c	α, β, γ
страни на триъгълника	Височина на страната a	Височина на страната в	Височина на страната с	ъгъл

Формула за лице:

Формула за периметър:

Правоъгълен триъгълник

Неща, които трябва да знаем за правоъгълния триъгълник:

Правоъгълният триъгълник се състои от два перпендикулярни катета и хипотенуза – най-дългата страна.
Дължината на страните може да бъде определена с помощта на Питагоровата теорема, а големината на ъглите с помощта на тригонометричните функции.

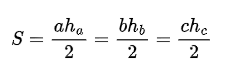
a,b	c	h_c	α, β
катети, сключващи прав ъгъл	хипотенуза	височина на страната c	ъгъл

Формула за лице:

Ъгъл:

Формула за периметър:

Питагорова теорема:

Квадрат

Неща, които трябва да знаем за квадрата:

Страните на квадрата са равни и съседните страни сключват прав ъгъл.
Диагоналите са равни по дължина, разполовяват се и са взаимно перпендикулярни.

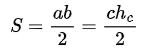
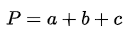
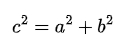
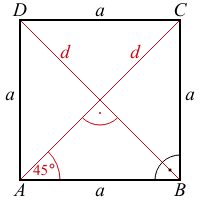
a	d	О
страна	диагонал	център

Формула за лице:

Формула за периметър:

Правоъгълник

Неща, които трябва да знаем за правоъгълника:

Правоъгълникът е четириъгълник, на който всичките му ъгли са прави.
Срещуположните страни са успоредни и равни по дължина.
Диагоналите са с еднаква дължина, взаимно се разполовяват, но не са взаимно перпендикулярни.

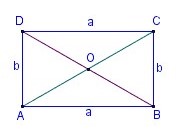
a,в	d	О
страна	диагонал	център

Формула за лице:

Формула за периметър:

Ромб

Неща, които трябва да знаем за ромба:

Ромбът е четириъгълник, чиито всички страни са еднакво дълги, но не сключват прав ъгъл.
Диагоналите не са равни по дължина, но са взаимно перпендикулярни и се разполовяват от пресечната си точка.
Височината е перпендикулярното разстояние между две срещуположни страни.

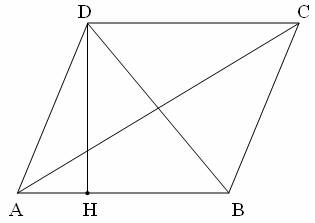
a	d	h
страна	диагонали	височина

Формула за лице:

Формула за периметър:

Успоредник

Неща, които трябва да знаем за успоредника:

Успоредникът е четириъгълник, чиито срещуположни страни са успоредни и равни по дължина, но съседните страни не сключват прав ъгъл.
Диагоналите не са равни по дължина и не са взаимно перпендикулярни, но се разполовяват от пресечната си точка.
Височините са перпендикулярните разстоянията между срещуположните страни.

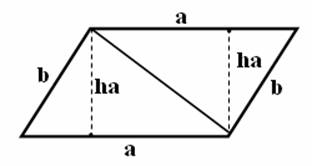
a,b	d	h_a	h_b
страна	диагонали	височина на страната a	височина на страната b

Формула за лице:

S = h.h_a = h.h_b

Формула за периметър:

Трапец

Неща, които трябва да знаем за трапеца:

Трапецът е четириъгълник, в който две срещуположни страни са успоредни.
Успоредните страни се наричат основи, а неуспоредните – бедра.
Диагоналите не се разполовяват от пресечната си точка и не са взаимно перпендикулярни.
Височината е перпендикулярното разстояние между основите.

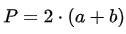
a,b,c,d	d	h
страни	диагонали	височина

Квадратни уравнения

Степен,
степенуване

Намиране квадратен корен

Пермутация
(Рn = n!)

Комбинация

Вариация

Преобразуване на дължина

Преобразуване на квадратни мерни единици